This line of research has been developed in collaboration with Manfredi Maggiore, of the University of Toronto, Canada.
A virtual holonomic constraint (VHC) for a mechanical system with configuration vector q is a relation of the form h(q) = 0 that can be made invariant via feedback.
In the past decade, VHCs have emerged as a valuable tool to solve motion control problems. The virtual holonomic constraint paradigm is applicable to an array of motion control problems. VHCs can be used to make a haptic interface emulate the presence of an obstacle in a virtual environment or, more generally, to constrain the operator hand to move along preferred directions and to sense the virtual environment. In mobile robotics, VHCs can be enforced to make a group of vehicles move in formation. Camless combustion engines use actuated valves in place of the camshaft to regulate valve phasing, thus allowing valve phasing to be reprogrammed on-the-fly in order to optimize the operation of the engine. Controlling valve phasing corresponds to replacing the mechanical constraint imposed by the camshaft with a VHC enforced by control. The use of VHCs in place of physical constraints allows greater flexibility in the design and operation of mechanical devices.
An Introductory Example
Consider a mechanical system given by an unit point mass lying on a plane. Its position is defined by the vector q (that is its configuration). On this system a control force tau interacts with the particle, then the system is underactuated (we have only one actuator and two degrees of freedom). The distribution of the control, F(q), is given by the following vector field, F(q) = R(a) q, where R is the rotation matrix associated to the angle a, which is an assigned constant.
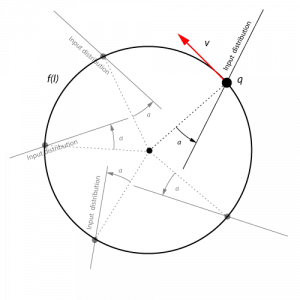
Let q(0) = (1, 0) and vq(0) = (0, 1), we want to enforce the particle to lie on the unit circle for t > 0, that is, our virtual holonomic constraint is the following relation h(q) = q’q -1 = 0. A VHC is, therefore, a submanifold of the configuration space, which is made invariant by the control inputs. In this example the VHC can be view as a parametric closed curve f(l), where l is the parametric variable (the constraint is satisfied if q(t) = f(l(t))). Intuitively, in this example, the VHC is made invariant if it is possible to generate a suitable centripetal acceleration which maintains the particle on the unit circle.
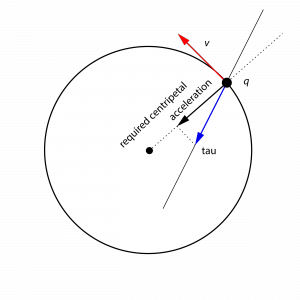
First question: which are the conditions that guaranty the existence of a control input enforcing the relation h(q(t))=0 for t>0?
A sufficient condition is given by the regularity property of the VHC. In particular, a VHC is called regular if the distribution of the control inputs is transversal to the VHC. In this example, the distribution of the control input is transversal with respect to the unit circle if and only cos(a) is not zero.
Second question: how are the dynamics of the system subject to the virtual holonomic constraint?
In this example, the dynamics of the system subject to the VHC (called also reduced dynamics) can be expressed as an autonomous system with one degree of freedom. In particular, the dynamics are given by a second differential equation of the parametric variable l.
Third question: can the reduced dynamics be obtained as the Euler-Lagrange equations of a suitable Lagrangian function?
Not necessarily. For example, when sin(a) is not zero, it is not possible to find a Lagrangian function on the unit circle such that the reduced dynamics describe the same dynamics of the its EL equations. In this cases the control force do work on the system and may decelerate or accelerate the particle in order to maintain the VHC.
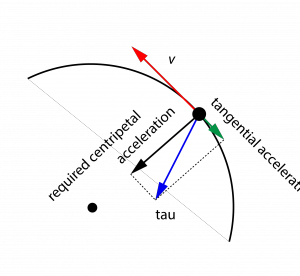
The following animations show that dynamics of the particle varying the angle a of the input distribution. The particle is the red dot on the red circle, the VHC. The red arrow represents the velocity of the particle, the blue arrow represents the centripetal acceleration due to the control input tau. The green arrow represents the tangential acceleration which modifies the kinetic energy of the system.
a = 0
a > 0
a < 0
Research activities on VHCs
Synthesis of VHCs
The group has investigated on procedures for the generation of regular VHCs. A regular VHC is a VHC which is stabilizable with an input-output linearized feedback, and possesses well defined reduced dynamics.
The group has developed two techniques for the generation of regular VHCs, focusing on the property of the reduced dynamics. The first allows to generate VHCs with Lagrangian reduced dynamics structure. The second technique allows to generate VHCs with reduced dynamics possessing a stable limit cycle (if it is possible).
The following animations show the dynamics of a pendubot subject to VHCs generated by the first approach.
The following animation shows the dynamics of a PVTOL subject to a VHC generated by the second approach.
Orbital Stabilization of VHCs
Focusing on the pendubot, the group investigated on the stabilization of a specific orbit on the zero dynamics manifold, preserving its invariance. In case of Lagrangian constrained systems, there exists a first integral that can be viewed as an energy function. Given suitable initial conditions, the orbit lies on a level set of the zero dynamics manifold such that the value of the that function remains constant. The aim is to stabilize a target orbit, that corresponds to a certain value of the energy function, taking into account the lack of control input on the reduced dynamics. The group presented two different approaches which dynamically change the geometry of the VHC. The first approach, , is based on the transversal linearization, while the second one, is based on passivity.
The following video shows the orbital stabilization of a real pendubot in order to perform the swing-up (from low-high to high-high).
Coordinate free approach
Work in progress…
Example of a spherical pendulum on a cart.
Inverse Lagrangian Problem
Work in progress..
